Teorema del emparedado

Es un teorema usado en la determinación del límite de una función. Este teorema enuncia que si dos funciones tienden al mismo límite en un punto, cualquier otra función que pueda ser acotada entre las dos anteriores tendrá el mismo límite en el punto.

El teorema o criterio del sándwich es muy importante en demostraciones de cálculo y análisis matemático. Y es frecuentemente utilizado para encontrar el límite de una función a través de la comparación con otras dos funciones de límite conocido o fácilmente calculable. Fue utilizado por primera vez de forma geométrica por Arquímedes y Eudoxo en sus esfuerzos por calcular π, aunque la formulación moderna fue obra de Gauss.

Sea I un intervalo que contiene al punto a y sean f, g y h funciones definidas en I, exceptuando quizás el mismo punto a. Supongamos que para todox en I diferente de a tenemos:

y supongamos también que:

Entonces:

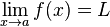
Fuente:

https://es.wikipedia.org/wiki/Teorema_del_emparedado