Dada una función f integrable sobre el intervalo ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , definimos F sobre
, definimos F sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) por
por 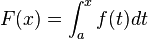 . Si f es continua en
. Si f es continua en  , entonces F es derivable en
, entonces F es derivable en  y F'(c) = f(c).
y F'(c) = f(c).
![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , definimos F sobre
, definimos F sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) por
por 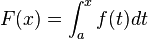 . Si f es continua en
. Si f es continua en  , entonces F es derivable en
, entonces F es derivable en  y F'(c) = f(c).
y F'(c) = f(c).
Este teorema puede ser demostrado de la siguiente manera:
Tenemos la siguiente hipótesis
Sea  integrable sobre
integrable sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y
y ![m \leq f(x) \leq M \; \forall x \in [a,b]](https://upload.wikimedia.org/math/1/e/1/1e1b2ad811ce2c15f191c634ded2afd9.png)
 integrable sobre
integrable sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y
y ![m \leq f(x) \leq M \; \forall x \in [a,b]](https://upload.wikimedia.org/math/1/e/1/1e1b2ad811ce2c15f191c634ded2afd9.png)
Entonces 

Por definición se tiene que  .
.
 .
.
Sea h>0. Entonces 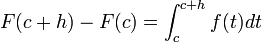 .
.
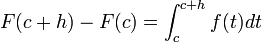 .
.
Se define 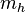 y
y 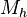 como:
como:
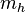 y
y 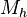 como:
como:-
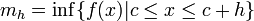 ,
,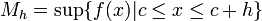
Aplicando el 'lema' se observa que
-
 .
.
Por lo tanto,
Sea 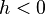 . Sean
. Sean
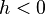 . Sean
. Sean-
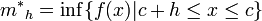 ,
,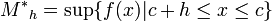 .
.
Aplicando el 'lema' se observa que
-
 .
.
Como
-
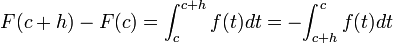 ,
,
entonces,
-
 .
.
Puesto que 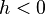 , se tiene que
, se tiene que
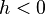 , se tiene que
, se tiene que-
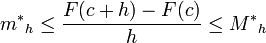 .
.
Y como  es continua en c se tiene que
es continua en c se tiene que
 es continua en c se tiene que
es continua en c se tiene que-
 ,
,
y esto lleva a que
-
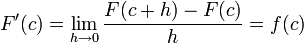 .
.
+




No hay comentarios:
Publicar un comentario